Identifying and promoting mathematical reasoning in primary education

Almost without exception, every mathematics curriculum framework emphasises the importance of promoting reasoning.

It is at the heart of the subject and is not an optional supplement to the curriculum. It is the link between learned mathematical knowledge, understanding and skills, and the use and application of these to everyday life. It’s what helps students make sense of mathematics and appreciate its relevance.

Mathematical reasoning involves thinking and working logically and creatively in order to gain a deeper understanding of a mathematical idea and to make connections with other ideas. It involves, but is not limited to, the key skills and processes of:

• identifying and describing;
• exemplifying and specialising;
• reviewing and improving;
• comparing, sorting and organising;
• generalising and hypothesising;
• explaining, justifying and convincing.

There are three main types of reasoning in mathematics that should be the focus in primary education: inductive, deductive and abductive.

• Inductive reasoning: uses observations, patterns and specific examples to make a generalised conclusion (conjecture);
• Deductive reasoning: uses facts, rules, definitions or properties to make a specific conclusion;
• Abductive reasoning: uses inferences and speculations to form and test a hypothesis to make probabilistic conclusions.

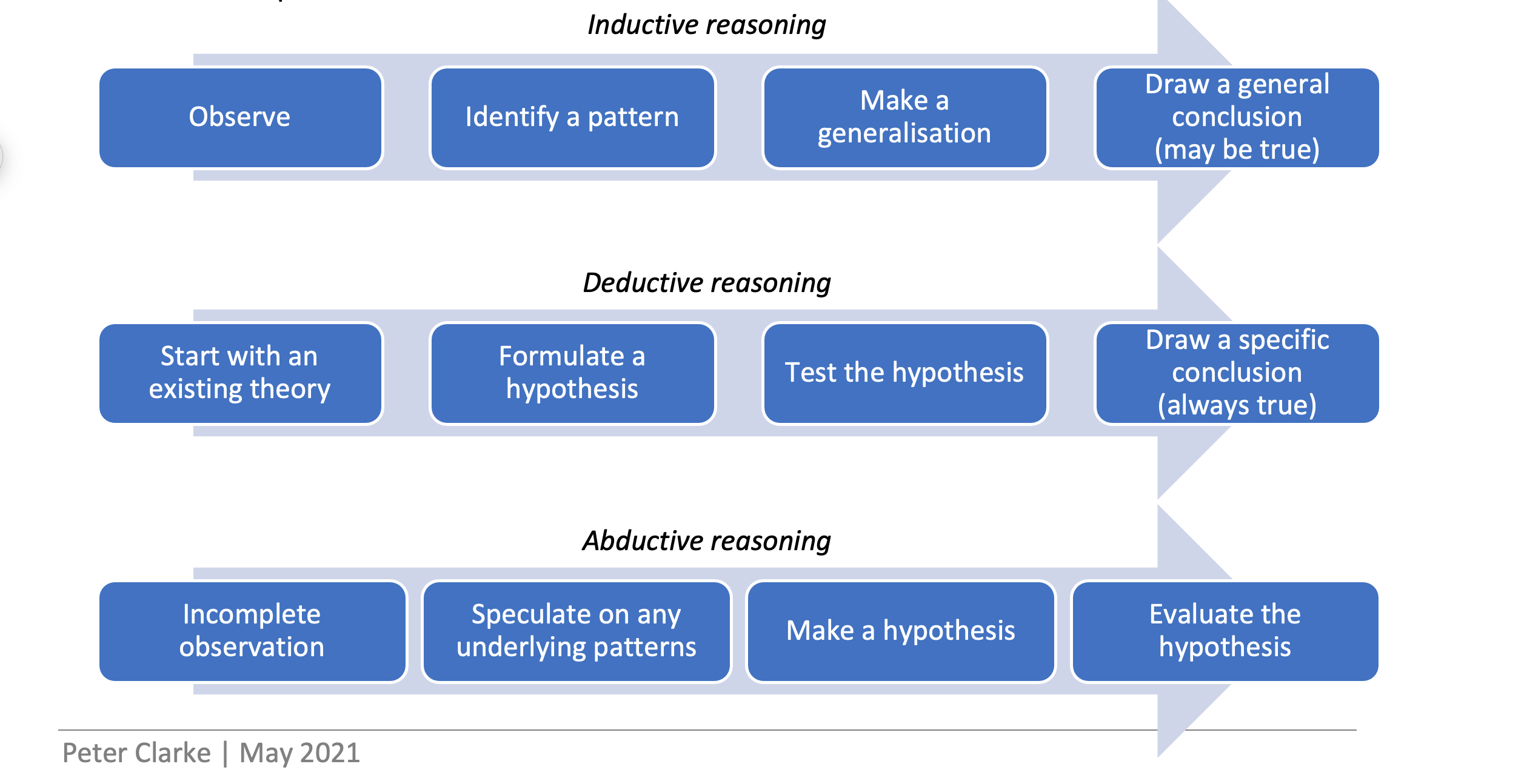
The following diagrams illustrate the differences between inductive, deductive and abductive reasoning and the different processes involved.

Although progression between these three types of reasoning is not linear, and should certainly not be taught as such, most students start with abductive reasoning, before moving on to inductive and deductive reasoning.

One of the most effective teaching strategies to elicit students’ mathematical reasoning is through focussed questioning. However, it is not simply asking more questioning itself that is necessary, but specifically designing questions that help to draw out students’ prior knowledge and encourage them to move beyond just explaining what they are doing. Ultimately, it is also aiming to encourage students not only to answer questions, but ask them to each other and importantly to themselves!

Another powerful strategy in promoting and encouraging mathematical reasoning is to provide students with sentence stems. This gives them the opportunity to respond in the form of a complete sentence to effectively communicate their mathematical reasoning. Sentence stems also provide scaffolding to help students get started in speaking or writing without the added pressure of thinking about how to correctly formulate a response. This then enables students to focus more acutely on their mathematical thinking.

The teacher prompting question stems and student sentence stems in this table, organised according to key processes of mathematical thinking identified above, can have a real impact on promoting and encouraging mathematical reasoning in the classroom.

Understanding the potency of reasoning to make sense of mathematics is critical to helping students become autonomous problem solvers and mathematical thinkers.

Students must be able to judge for themselves the accuracy of their answers, they must be able to use and apply mathematical reasoning skills and processes in other subject areas and in their daily lives. They must recognise that mathematical reasoning can be used in countless different situations to help them make choices, reach decisions and draw conclusions.

*** To share your ideas, insights or expertise with the ISN Community, please email us at [email protected], or send your draft article directly to our editorial team here! ***